Beta vis-à-vis Correlation Coefficients - how the two measures differ
Intro
As you may or may not be aware, we specialise in lowly correlated investment strategies. These are investments that move largely independently of the general market and are less concerned with the ‘rising tide lifts all boats’ phenomenon.
Correlation is often misunderstood, poorly defined and confused with beta. Whereas the two statistics are close cousins, they do not measure (exactly) the same. As they are both very important to our process, we feel a primer is needed to alleviate the confusion that may arise when reading our research.
The techniques in this note can be applied to all risk assets, but we will assume in the following that we are dealing with a listed company (“stock”). We will also assume that the benchmark to measure stock against is the entire stock market (“index”) but, in principle, any return series could represent the benchmark.
Before starting, I would like to stress that, in periods of extreme stress, virtually all risk assets become correlated, at least temporarily, owing to the ‘flight to safety’ that affect asset prices during difficult times (Figure 1). In other words, over shorter periods of time, the strategies we invest in may not be as uncorrelated as the theory books prescribe. This deviation from longer-term averages can be difficult to escape when financial markets are in flames but, given time, correlation coefficients always normalise.
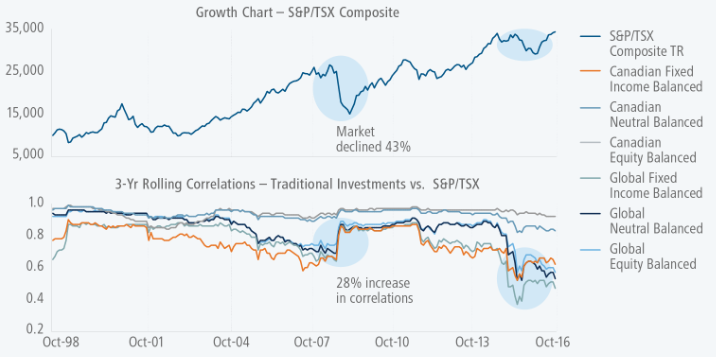
Source: Mackenzie
To continue reading...
Definition of the `beta` coefficient
If `Delta"stock"` represents the percentage daily change of a listed company (or portfolio of listed companies), and `Delta"index"` represents the percentage daily change of the market (or any other benchmark you wish to measure the listed company against), `beta` is a measure of how volatile the returns of the listed company is relative to the returns of the market.
`beta = 1` : The returns of `"stock"` are precisely as volatile as the returns of `"index"`.
`beta = 0` : The returns of `"stock"` and `"index"` are completely uncorrelated. One also says that the systematic risk is zero.
`beta > 0` : When `"index"` is up,`"stock"` is also up – how much depends on how positive `beta` is. For example, if `beta >1`, `"stock"` will typically be up more than `"index"`.
`beta < 0` : When `"index"` is up, `"stock"` is down – how much depends on how negative `beta` is.
In Excel, `beta` can be calculated as follows:
`beta` = COVARIANCE(`Delta"stock"`,`Delta"index"`)/VAR(`Delta"index"`)
Definition of the correlation coefficient
The correlation coefficient, `r`, is a measure of the strength of the relationship between two variables - in this case `"stock"` and `"index"` - i.e. how much of the movement in one can explain movements in the other. In other words, it is a measure of direction, where `beta` is a measure of both direction and magnitude. `r` is never higher than +1 and never lower than -1.
When `r =+1`, `"stock"` is said to be perfectly correlated with `"index"` and, when `r =-1`, the two are said to be perfectly negatively correlated.
In Excel, there is a simple function to calculate the correlation between two variables - in this case `"stock"` and `"index"`:
`r` = CORREL(`Delta"stock"`,`Delta"index"`)
In Excel, that simple formula effectively performs the following calculation:
`r= (Cov(Delta"stock",Delta"index"))/(sqrt(VAR(Delta"stock"))*sqrt(VAR(Delta"index")`
A few additional comments
The difference between the two measures should be relatively clear by now. In simple terms, calculating `r` will provide you with a tool to diversify away from risks you may hold in your portfolio - in this case market risk (sometimes referred to as `beta` risk).
Meanwhile, calculating the `beta` coefficient of a listed company may take you one step further, as it will provide you with a good estimate as to what returns you can expect from the company in question relative to benchmark returns.
The two measures are closely linked, though. If you express stock and index as standardised variables,`r` is the slope of the best fit line. Meanwhile, `beta` is the slope of the best fit line if the variables are un-standardised. Standardising them just means expressing each variable as the distance from its mean divided by the standard deviation.
One final point:
`beta` and `r` don’t always move hand in hand. If a dataset delivers a relatively high `beta` but a relatively low `r`, the data tells you that the company in question is more volatile than the market, but that the two tend not to move hand in hand.
Likewise, if `beta` is low but `r` is high, you are told that moves of the company in question tend to be highly synchronised with market moves, but that the company is less volatile than the market.
Niels C. Jensen & Soham Shah
16 September 2019

